
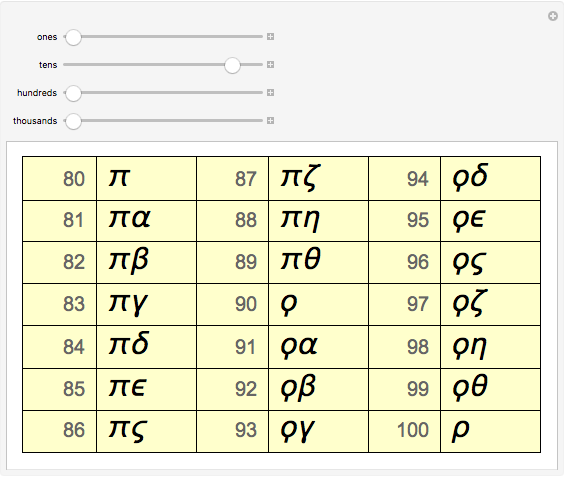
This alphabetic system operates on the additive principle in which the numeric values of the letters are added together to form the total. To distinguish numerals from letters they are followed by the "keraia" (Greek κεραία- insect antenna), a symbol similar to an acute sign ( Unicode U+0374). This requires 27 letters, so the 24-letter Greek alphabet was extended by using three obsolete letters: fau ϝ, (also used are ϛ or, in modern Greek, ΣΤ) for 6, koppa ϟ for 90, and sampi ϡ for 900. Each unit (1, 2, …, 9) was assigned a separate letter, each tens (10, 20, …, 90) a separate letter, and each hundreds (100, 200, …, 900) a separate letter. The acrophonic system was replaced by a new alphabetic system, sometimes called the Ionic numeral system, from the 4th century BC. The earliest alphabet-related system of numerals used with the Greek letters was a set of the acrophonic Attic numerals, operating much like Roman numerals (which derived from this scheme), with the following formula: Ι = 1, Π = 5, Δ = 10, ΠΔ = 50, Η = 100, ΠΗ = 500, Χ = 1000, ΠΧ = 5000, Μ = 10000 and ΠΜ = 50000. In modern Greece, they are still in use for ordinal numbers, and in much of the same way that Roman numerals are in the West for ordinary ( cardinal) numbers, Arabic numerals are used.Īt first, before it was used more, the Greek alphabet, Linear A and Linear B had used a different system with symbols for 1, 10, 100, 100 operating with the following formula: | = 1, – = 10, ◦ = 100, ¤ = 1000, ☼ = 10000. They are also known by the names Milesian numerals, Alexandrian numerals, or alphabetic numerals. Greek numerals are a system of representing numbers using letters of the Greek alphabet.


 0 kommentar(er)
0 kommentar(er)
